Skip to main navigation Skip to main content
  • KSPTM
  • E-Submission

PHD : Parasites, Hosts and Diseases

OPEN ACCESS
Search
Advanced Search
ABOUT
BROWSE ARTICLES
FOR CONTRIBUTORS

Articles

Page Path

Mini-Review

Modeling the Dynamics and Control of Transmission of Schistosoma japonicum and S. mekongi in Southeast Asia

Hirofumi Ishikawa1, Hiroshi Ohmae2
The Korean Journal of Parasitology 2009;47(1):1-5.
Published online: March 12, 2009

1Department of Human Ecology, Graduate School of Environmental Science, Okayama University, Okayama 700-8530, Japan.JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

2Department of Parasitology, National Institute of Infectious Diseases, Tokyo 162-8640, Japan.JFIFddDuckydqhttp://ns.adobe.com/xap/1.0/ Adobed     ! 1AQa"q 2#w8B36v7XRr$9bCt%u&Ws'(xy4T5fH  !1AQaq"2B Rbr#u67Ѳ3sTt5v8Sc$4ĂCÔ%UӅFV ?_Aנj- H>>,m*>fzp"TrKkr^r.|_&]|*vPuܶvoQ1mwVJUhu-I"=LniAƕ8"۲ k*ҿ[yu:.vUQ+)%F DHyVBk>Hy8jݹ q~9D4KRmzQ)^ʔ.J%k_tVi5NTjg!'ky|5asOȻ)R۸ߩFMԿ3L4j6dڜ#NIwUF]JqB/(FafJRzq3\G՛ ?~\ 6)6W4m[O^L0E&rRMض*C .]Unl-1 1r#Rj/&QɈ׉˩s6Rj=5Tg.y.·Pӡ:JJS:C8-2u]d&vUz;7p9 5VnL֢"y)">iי(IDDd| Yj0; LRfS:ktYK%*N2^m|&dğth":ey)uPQZW)gcC3Pv&MMWd&Ŵ۲mvTRoժM03*F3Yd6\8,\hݻ kߔi<k NTwSԪmljj[>->ptU%'LR>&EBH$MQAUx[$Z6vi&_a.KIQ{hyƒ j"JOC9eFҝfj;˚Ω<[3_m% lQ@4g=5$(J]Yc-OMq<Ǎ wSzڗ)k$7VIP붾ͯnV+卵*t]iЎD31~SA1éC2u)ʼnQn-Uoi3:grI8ؓWm*G zܕ)ZקJ}Y YlGeJ6cB2I NS3Q>k=KTBT]W6+SOXQgGR? telˊ%-Re\hѯ2TF"C/OJΩ6r[N.0{SpljjX1“jOsӥ;ҭhe}xu`Ք&.)yO̒ Fߑ.$Qw;9Iw2o+RVJMSOj[SoҌZ%;`d$blQ{Ro{Imڌ>3egf\O֝Uzx"䢸g+mv%Gʆ:|V[N'&ס-ޝ'kfE|K,G&˳98Juin/\\Qݿ̋v~Ǩ!rtWU d|E߫R4d}.qPw*Ӭv5YEcn~f5c%MTMkb-F>5JT,})QHg%{("ӔȸWMsYyWNRrkkJr0XドnͫT}r-jj,Ŕʍ\Q2Ri>v$5!]"JB2WɅ)]VԜUc8i|.jeRO6^V.¸ Q&#|ܶ-*uOG%JAtRZRr]FFG\۩w+?'zչSѧt jz>KW&ot{7P&2D;&\\>Q2JzܗAKSfeNn[jRrԕf6,q,F1tRfԗ>vֶևj-&R'Zi2=xv~Elbsvm8=ӛ"ū񕜈BȩlWau[]ٷBߨF~J!|Ipr3R̴#Yp)={7:G{+:\W}n|Q#%)7^-h"Ƒq:M*%J&$T軨I333׎g_- ucBwwjp[6i25$̏bU’ٱRv?G\~#Iͪb7<<}Ezt" q_Inw,7-d,G÷%T* Wg1"䥱kq/A.,_KhqŒxwvo u2ۥۧ.bQ}XκA$֣ +K״ZUNmڸII{.v{5z5ѮRme[moyƾd~cRݾK'j.\i&/S6f|b=5: p!6i_ 4j6=.si˧eƾtS^c.Y^RJVS-Vi3,esi08?H$GvZgg?gi䤟2adw릿:"۪lkSN>q-4kI܋ێe̊qۅgDoѨ9; #T.Q;7#~_Ufstb_'w~Xw1Xk,vcOt._}v}8"(4Z\ۘgk?J?bm_c!g{HZV]Fkk%~gEt)b秴vΰB|꽸}mp~E6ݹv;7P٤v+ri*3Ԣ|'O14_~7nP{7ZU\Vű[ +7󖱅o#:ǥŬ\|3r%TJX]V7ez¨Y]lc|O3V! R zbJ'PnGqVJ"19WVeOF埜EaEJωqCN5Z g-9[S<$sUK5b|7sn\7x qmv##FF\ w[=-43$^ooVSiXօv7iB۴yg>]Vf"r$J3""32!Zh[K%7GvNLs+4nB/B{vlsobJaҺJR:0g%&zR\ S3T[&ִor*ⷳc3ʊO[iozW٨%$gn:ܶWwFBԹjHP&z u&F2\f;ipW73 [; '_̽b;vib!oec dC-tS__$Xs]l9&z$2/N>%'[}b{h/{`{Ji׉׏ YJB/X%}.|+{(S:qz]4_Kѵo`^tY_4S#* ^zvݾMr+TrkQ g.8Ͽ^i>ӈǙvix>$o( ^qt*&t1oJVu-ql5U6jCЉmĻ*"?JT=K'O/|=Vo}l0b}}f?X[?/\JSBe,kP8ETJ==?.p5ފgbU9}ǶdNKk—_$8̸͓ۍ8Di\BԿ-1v{FF]|.^ۅ{vl12׏z7-R7wE?\nh\jN/Kձr_oBw"N QMBZqe-m:ӨSn6j4%!hQ;sv'm4kcM=!8\m[M4{SMliۇ%eֽR&N:{2A8)THLK3Zj[jPBx#BگMf:G1\`edcʮ?|w(-̮vXt,bW2;.ιNHRR#YwTM"<;mk\.foIDjmlJ;vxy7o7i\,KQŊ9d^Mmgc L*.T6tLeIuOH3SJQ3=F/ʿ<9\JM6mN6=<{xkP!F1QR[I$6ُimXu2An2yԒMU q f[IB-'䤯jYm52&JG\zд\~vdg QtHGXw&1Lw+nDEdC1w|YJmvP)HZ>i0BPβә?R:QO["]I_Jʏۍ>QKyu^bycBq4lXF~l [\*N>-J6,Gq(Zr5h]CwYӤU~ʶߑ u*SIv%ZfJ7)! FS*s_\|IŸZ)J ]ܜi4"z[+Z,MOZ))}|Ʀ(RUNIII.S'ˍO~˨rn}M)xxӕ0 eyҵ7YMAB]ӣU:/ѭ*6bcwP͵ "+qēVjŹO|GtY4V j[mLV M -m>",B$ GD1~j6O4|LxnNmqATNR3ε|DŽa[fmn-ڭ+FiK7Pcm;r5 l8r{#-]'nrFh2ruycb;pW=njRqRJ(d mnpckNnʹ+6]tz~E=ʕ l ZZ5jSi3#47.Lcfe`9؏v囜.F\-UZ:*0_<Νu9Lӵm&)_3\^ҹ3"1n1v_|uRʞͫr'iȧN_kH׺8xXrj=\МH)V\ˬ.Xʸ oVRC}ySU9/OBY먌5 ٿwޞ)rw8Ӫi5*5ZΗcGƱ !ZۄlmpjJ -l <R̵/JAպZuq\IdUS 48wXJJtcg4cI~aqߓwŷrm-v)G7yS^7H^-\mŌAq|"m9IBnF㏉9[N+mmy/!KKۉ%n +BdddfFF6FQRN-U5;Sv'm4kcM=Mn)\qιqUd9F%",6MGdT%-+~ f%+y֛^3SrF>6lc(֪vۊN;g._0Sѧ]ETWرkQKzGe9ʨsKA"yC y2\[5 rԭ7Gk5Mzw_4sM3hxЊ'oÍ5jsub )ͪ~tR2H]R͍>̋m6=%(˿(Wrr-܅y5(ܔJ޺YunW̹븹NsqK ]/QR#"ZMDfD|43Qw|._ԡSqTZBg??O Ϥ)/E_U|i}2 9Z?¹0:x'3,whǣ?C y-A~=daJј&M?D1_PS+Oi&;a @;Dž7[ zZC"bv:jjMQk$M RԸ3uA\=wI.AwC"^.{?-\NSiˏ"b}T/}q/ o.1M}R%:-ZniʒL$SgrBW*,Mw'N\ɇ{s\j]VryG'8f`}'N<*/`U숻z CwHq18J+vԕKss4R53/&XTt1bZƟo\=%nO)h$rBi-nKĪ^ ջڜlwkYm[̑+/QrZo%TQ;TLs($2C:s.%+eoNttq۰kK7O0m_t_pZ1SsSM7"mevFZ[w -FJ*T*jФQRg BSu|]g:ɵzjqwmltL.e3sRMچkSmjkmWœިm++¦'tILk*բQ D,PB\lI[9{%Gb R6öۍmX-MaʉA931cs..G4CujQտ[9 }G-xwl)IQz j Ó"rqe&=]꾧֎c)<kӳ+0JrRR3'TnXi^xMF Bު*tIL.[h"2"nKzZe'ZV/RrNYz]8죝n]Ķܩ>^Ժ]u-7^\mZjܣ9+Rmn ߑv?oꋘ?&ƪy^N4o=3-ؔ̿*`}V݁ ƒPu8%$ ݗ]wt;\y\>='OjPIp/nJU8{϶FNMsf"ίNqƹ(+ ݮF2Km |jܴZs%zf*eȫ?]4)I۵nR&FX + [jDh(#哑9q9Eծj8noǕZf\J-l&Z˫}`ӎhyrΉn\űn]9pʌӣ"׮Wt?N4_I_~54#/my1Xr*척aS#DT >q ssΛW;3oUaJSRMDgQnt:Ql,/ ܷfRqiM Ȼ>Cob;A>ڦWقM9X~/!'MW.}Vrߔꔵ!5|iB(0-zF=}okڢE$^wW~nokY߮\6՜̌{i-AF*9)\t9IV6۸5ZUF6R$ŨQIq砳YUZ]eyv >hI櫥N )&l JulwE1GDOuFN2| }馥uC1rޫV+^gdb&W[4<^e4YW,d|htͮsUM)۸8:{3d{AѢ)~ \#J=NdƮꮓ90 |1K$v*?мS ]i$J,C,SG?/_՜pMSƯM|mG1V1$~K>CSvkuj=&) -,yLjuFHK{c駗.SOua;BrSqj-ۍZ#'Jys7[g2z/.u4+XV2VQ.ޕ)$"(%)#Z7suZ%j }BǬݕe)Jvz8zJf:hIN|svO1O#IEcۍjݽ:SdὮvu^@:o^5cs>i/VqmVm]ؔܢn6'vޑ̗J4Wn@OlKbX ;n:hgJ9ŻyǑz8f܌q&Y fN0N;[69 rbׅC2/#kE l&2~èMR.*%g=Ft.%؝e8<.e=Uv{~㻏"EˑnvDѭ͜Lu3u0:U֝$[M5<:oi+V4V9 6nXvx&_ q Qqw3W:uϔ2yb/(ɳ|5zQiJ#r|Hw#.W?4aDŲ\ugWG;Cw鐢K|xg)##=O.dF˟jMUvWĻsr.z]kPc9"]R)mkfOd*uYf١RsB Aîh=k]ʳUrrZsq`d#r$/Ը3o^&lRWȍyuW̦Y4QDUMJ65ƒ[+ygk XK_±k#y:8(TJOSQhJt2.DR}"5[) r)6V6u5k:eXZmv𭤔!푊Q[qQ}ҹLE- 8qIZG|UM4j}Mܕ[Vwm{} Naqµ"ԈM zOpKѰ?IAD3Ir0'/q1itoB5{%wkOBn-ۜduqIzYK60{+DʕܞqIt";r1mG/\/ym[6JƫR \L=S=OT@Ix[TMm{>ݾտ֒ݸӉLYIx>+"JVNzx||5rI?C{oz8۹e\R-^\A2F R+N9 vlT]"ۭ d)t֞i #E2jB@׵=#/N+!ĕhx}I!cM`ąZ*ŻɄҒ߮Y.Z}='/oۙ3IpW̮hT7cTSuz9>B}΄&h!>lӵn~j˅IvU.'v'CSZw8QK3G> ,J59ٷ+HSg䧎hJdzvwv-cvxS5[̊n~ؿ%ַX?O0\6ne 6kn9.ϯ} *h 8_QhLݣ7q +=XBҲ5?[[)+F`=4 }B,sNg==u*Nj9k_GJ)+R~GSPBȒZ:(K]heL=vKPӢwq(NrG^ثϣ?#tC?.ͼ[ۅo؞y#%ǛjVyLSw%T*s92JTM%"YkQО.q)gCͲn8cgi6j1MѾ[{9h^vƘǚםidfi.^RHmg&rׇz:}݃}xT$ضk'5s-狶,\vpbPD،=Okf.c#cdz2FK5T!&)|ntD<+OŹU i-G[EE*FDfeaf2QƤM\UG_{ǹm%\yrGy:.\4wjPGUJޕUV7Do\7Vy_13w;[?c]H\$IJ,*L]3b%L{y.JRKG2sq,B6T}(#nW|km+q5] r㪍bJ@y{byz,b踊3ϻJ,'^xd،)JVw#.Vټc''ÝպWtbRؒJz۠8!o9IۄS95E9ؔ-e9JR{dmnｯ<[~n${~Њ$W?&ՐY_? #a.ߑv?oꋘ?&ơ|y^N4o=3t=~7!/M3>n8W홎2M`Qx+ z qy8%]7_~540ۦ彷]Wq CѡwkďyF5Dum_}~P(5.(X,K9vᯐ?leB9;Jhm#3{CxGE-S{;@Fz˙]=O'!ɿ]' r`:7'2bЖ>Iy,/eTy/V<.H?UYY{\^#ѣr9^7?xoRȆ7EoS_&??zϾM?(~Q-K&>"~aߨ t7Emsϛ+?;fCr)fY+>z$tIkjn_>vnrֳki-˹l= t;'EyC¥|/BLwBJdgjۛ$s S1|ɍV%JI6KvəhzIlBYɒ|0"Sy0F>eo5W)O+X˻u';v)2vVq۳kۮws?UʑBǴYO漪e2MIjPAک\b1)DDؚKm6ZWΨgȕ۶yjڳ 2ضN[C[|r@9Jfo<_eI7q.|cÊV߷:i.:$ȋ)1%%)ADZCEBxJ0MJۥy(bNsKM9k43IwNt.\%N簤I'.j|ƃ2$grBEٌ\}9:v*!n7M(ɽ]7c@XxƱԨ37īf62cTTfFK]9wntQHͮvٱI/f|j=7}\_V5U^+:uljSȃY(XI.ȱmo1甅jڎIZ2>#\*:gY|4k\8ZwSqtyA!+];бޞKծË¥e)#5ap.QK^8VdU{*ѽL\=qmjnB5>{ Ӟ`v±5 ^k&O~Oshɷ,;6nOW>u6{RqS`)S%jp\ipdEBLfTWy$GIYw~䲭J.1vSY5z.V>^+Ǎvc.I[R{QsNR3ӎfhd>y?UJ*}~[e\i5U^͛E]G_FS(Iɿ]i8:4zj~շsW,ˆsy:%O}iur]iF5~3M:Ӟ#N06)4ߧgdawIotiz:1r5YDZLHBSi;NQc44la=Y kQIT*ըl:tq2(է9VO4뒳܂~2rq'nrVZŦ[t7\oլfb/mlpc.I8콚q^1iE~䰳mi[dۧw֤ICfdFeCsg:i| 6擣׋* 96lust^{%99UNRvaMܽo ammi$em4D6DD\nA%$$#}۷/ݕr99JMն[oT޲E"KTaP+HGkŴj5TM5xƱOS-k`ۛkٝWz;{kS}F;~q|~^_|euwnE'pSupUP)V]vE+t =ZRaVdG6= *.ϼnj9:UɷbېmF_tޫgHjVS'śǕًdkkѻ_]Kv?nT>)^e=Ar1'3ԔILyD?:-^in):{7.؂\.:V }#뺾.3r̸*xbFM aȵz 6SQ:ײj[ 8nn iFMw rR"5M5I旘35f^j='j:nNW.ʭocZvZKV^ɚJ.cM1ZI7E'6rg탸5oZ=[m Z`\hbMUR١Ȗĉ):Jin!_7Dй+f̷eKҷvͨBPR(V`y6tw*MRΝcB.ڭTnc;P$8nFvm4(D(R#R-L -2:FP lxZKQc6I("Km%$E, 78uXIFA$RQI$JbInG]c[ֹ:ZM+n^')JmJMJRu{e)7jQDw~%yQl}BZujSSf۩QZ+Dzhd5o%BIc'GZ?}΍:>Ɵivז-%݌J5MqGWTVʦh݇ܟ~Օ_6 n'{3~mϬj'J11OȻn߃r Qr\3y٘+WӍ'WxEs^O3 o~[|7>]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%-(\D4h{UK&ӡn^m]Fݢ:`δvj俜F+) y[{{ 7 tu>gvrěOj'5 iRg[ͶFjGe n~qT$ci ۚ0oԹc*jL[sVWqj\ݻ&6"WoK:cnWmrv)o>66(F>=W^bf#c zzʞtپy%mՉPël e}J.\Zk4ttt>oEM=q)hJjI=ͥ(%]脼_88ф;͛gWG;Cw~˘$4=uWdĜTثNDkiQL9U*O"4XP`02,Ge-k5$h>ܼ]3vr6!9RQPIVSnM(ۓ{>;/Qͱv{3&-[rc)ܚI$n{Sv3[j00)-D3z}MRzVQпj,T[uVs0\}Sid;r(ݝJ>æʺL&c[jPK0~d(FKÝW\m]GTcF|Iׁ)I3~#oX%vҦEݑؼ5Żv2qAZTE^..M{ʐfȏ2##.R}*KʛZz^ӞN*lPťLf\G6[WVQquV]XAi)5J!,$iJ6o$tPZc;Kjx_n3`qIelV~vLy{fn匋Ѿn%;zV.n'-ұdd2߽1bZksPe3TI9)$ԩIN9Vơ\=2885N\ p)/a柛w9g_lױo8ݷ iixJV& ғRi{N^_oAŮE6Y7I$Nk$|Q)-*4Z)^¸%4Qm [I%.c-OV+C֧R#%ѨCe3i;w$G+_dy| Fzj$DI(=OA gj%v/]8qԯNIS*֩',Q%\44ZZ%D|Ǧʴ6&vֵI$%8(ԬƾS&#Z. }6z?b/|Jl{ץv&mpx4Z$”ڝ4-H%dGKfM:sKSRWeJAn]>s6应-W9'H]'uȫYvgK^\czp|My\鏩w/ËQ.)]\QiS`8uL뚛̸=J"ܻi\å'-)54Ue]:K\퓡vK xwBqrH\*֕TnzC.mT=t-H]SČ~Nu╏NÅ3f|͡G~B+Xm[Q7U{9"~jgK Zoʰ7"qJ,ekSeNGgϳ] ^.6:s}_,%eRg<5⿨z{ZPun#jRІ.6g T.!]xa c#jN$Zpl̋H WZu8WmMRýsĮ?Mco~sx TU҆Q :KDG4n42.<3/'^?6/ܠڒ^yrrÿr2\D}}B]^E~^T cɛ7϶Y[<֞[7d}2%QPqOLEQR\CIsj1?\}%tJ0e~ *sk"*)&ۓEi#{1J8Hrt|'ܝRr8)=ƔN'RVz:cf]F7bZyZUȘ4x8,#JG̒?.W9XnO]KO]%]ƻ O5Γ/3qÓj؍/r̺rƵ 5\&m6h.xoeX[=<3%< lZ"2h\Z[&jW3ejm?k&[]ųj+{N{66leu_+lj]q* 7g*knأYv= q ەdxЬZ|%GUrQ3jLŒqET]1% qkXYūYc[7Ś]QY\jko\</Lc7+'hMSUc6qXyؙ~6#ѯv.0$BQi5YyIhɍiy=KD!n3Vm[V%W-B%swa97ajۗ m+9~]fKq|Ddaˑ0A]_v޺mM5* F-BYHJ5}q>ʉ.6hyDmpD׬'-_v5;5[8K[viJ.3dR:oYHHh9I7:۽fi+wm^ [)odPѱ52CZUJicSw\&_s0uBȍh32džzQflcd^m|7GѹE!fO5]]H9݇ZomT@]?5B:Z߂'`V_+/MSKX߆ޠk3?o7y:4R/7þ] iG߬aBRU&?r&/} cQߥGj2?C5Yśe7hU=?+ x龳f-܈czW^7p%5|Y:SJE\U-(a_cƣUǽXXKiȞNlmۊڭڄR!**ܤMeȽ$|X5(Ź\rJ~ܮ]>'HB0cp XFr_c?f?7<ukSgov¥iG>>䙗i.+t+bOjIܶ . i^:nm}s}(3>NZ$2Qg([".>i.ƾ)B̋M8+"- >eE6DݥJnJˣt׻ 5.˅nJGwZD~!i۶a,Db3ZQ3O#KO5/֍ozuK'GbRi᝘NV_ҝcvם ZoX}F6z 7e5_e:ۓj=AB+iܔERadMBq*ԯ DwI/Gy*mĥiRKg6skY/#SN4e$-yXM YL?^ĸNNӪ{$r1JJRSLO]Aqm>V/s[~i/j+m>z}eI"Qvp]{ZԼ:{vPAG2=T͡@ڐ#u"E*>C;o$~C#_d/HBq^YRٽzIKbOm\~żjFFGdiQ(*/i*#.FF]©m=BmpQQQSP&Ҫ!T&^>:y)$ˑÐFčI Bӡ-t!bM WҦŶ'UZ=}zvn~oT/\ǒ'nr8 AJIӆz<^uߖ4eFC1i+v!3qNyߕni?4JZlmYFXFۼO0B\m[ tʄU3s"Sr(NJ;SKW72L4̏BVdf^Ҹj\]ȱ۪(ӷm?J-KEmWڽ^4<8qu%9pŹW~877ܾeVгS(յe^C]yX͹! םm4FGȋ\y'Z FX7e)|Gjt߹#gb\ŧq_([R8[qU$Z (ʻezV2V!iQ,i$JE˂٩ a(GK'O{vnBvryRd-RK4=qxZJMl_CuuIz @Rt㮽޳!|68\-l[џ84-2Pu" RJ_^OL>G1~XnBŬw6J0*Uvlږ1N G1q9IUm*'oWu][&UyYZbBZRZNfEJf"+2nF~Eû7n1xv.RUM$6 lAxSQJ&n5ܞwlEói"#>4׿Q.nEq7Oko[1wg8ZQwZYiqtm&~">Bo?w͡ni2峋NCEy Ҕ+%ZJ ʩq*fpˤl,~^Mχk1+:ݕ z&Y`KLӪУDr3[*Z :(SL&ݻ۬Vqsyԭs x|iI߽zZrg.:mp%6ԜvgmpIUt;QbS.Է) ǨKSV,*lڌ|5Jt3#NP.=+OZ~/G سIgbꥹJnl_DUM\iM!֔wVZuԺ,yV.Q>f v:݇WiaŸN5Ҕ[M7SsrvǣrMW= \8ZW-jsnڕ.ZnF2qt ً[ٻޘY۷Zm"Jxr&NAfA-݌to9s359݆mZ+N1-qS$D=17 x׵+%_ ve4ir6Z$FDڗnFtOr'7'{9C˨ꤡaYoace{Refnft RR"4%ʌm:Sj3)OdInTO>X'vxV#jܮw9Fog;5.~Y5\~18YQܹvj4+~t7S ﬕs %^۵ڴDZV69R^Y+rj$ԇoJKR5wB9C>Y:l+EǎS{ʲ{T6Wi* ^^9k/y/Cs\g*qڵgn4T8mERr|Ti+iPe;;.i\EBEJ 丬i9ɧM-ԼsGDrZ>r#R>~X9y4b棇9JwV۔%m(b[Tjvl}۩~nDԺ{Zo-YuK1vx.nWuO+jN [ٮ0%"΢CdTJK-RަH"$I(*ve &҉FzB,_Vpqp9m8werv')E;o&QE׵^d9˦j\_,ڵugZȻ̧8k+jK{wmr@3ӭ2 wFkzFVqs1؛.v'I%$[iT]D5Dl2 nk7qUxԫLS+sا3/ΖeZYK<["%-g/kRs:f3;*E ت wJ%)5&+&rw*霣i|sMҴ|;R+fm䡩.!**dӶ-6s6,]zAXMWjmnz%SJߴm2UXw7MQ%<!tKys#P,W>s;3IYwx<+i_\\\U6 u7P|xbn_k&ӓVOe䦒 VUr,-㘘"-LZeOSҠթrEvq8Kf%5%&K"#%vD/.ZYYŏ+p$nZkvއuW9㓱Z G wYIFyf)?ƎUm5ԉ/'k84{KO:rQI}XRuԪ|*lu)3qZ[mSm5R3".Xcَ5c®ࢫI*۳~wRϿQWޝ(EJrri&ۥ^ʶ齲Im|[yb;mnm֩uiܘq>E+Ikx߄3r33-5𹻖09ϖ9[Tz~mr5NsWl$oPusޛ^{Z;);sڹf\3oٹZmԉ/'k84{NO:rQIBø8Bݱ3n֤DiK4u& ofSȒܩx<˘|N0Fչ]qsp"}! QWw@t4ӭ+cO5%]'*{eM߲DRO1y*q8w++e!c߶ܪlZWّM欼 CQ̼빶lX{vib/V/ ai;x6~]+z]MWB>re-:lgk}պ!#9?%܋V-c[z!W?c7YNm/jRr[HOzԻefճ0q15Zp#rkQQ0tU-AmڵP/cȕ?0cZYj;:0ZM=D6g ?'UN+ձ[K ܖB2'xq9{|۫N0ku 7xaj;n\ 2[VznMlWiKbSk))f..)Km)&bGZ=>OR܍W:j'rM'wYz&/鶧{Sʵb"vջq[I-ՌZH._x*BagC'T(Q:$ͳQcMCKy?3g'ߝqnT);qs #ؤZ}OOI:cfnc8W~qy.;^pVl]Hԓ>^H^@7-AA܃nmL(uWܻS߿ Td95Bdh4t6*dDh!EhI[iŨ\L.&Nc ܮf^;$R)\rip9I|ٺ?#R.ZDZ;/]nݻqs\QE9M&Bd ]N mN*D>tgbK>+ˏ.!23]BȔR1ɝ^j'k2ƮqBQq[$di]icV/e`޵B.FIIJqbi>Ӥ|p; 6${)RU>_e}^dzdfzi %ekRVUS?6'hׂ)5.\+qUgzE2C˷ecŏ^֔ibk shesFWJ#~> Wk~ݨ}ڶ>ơǚ)׽ZƉo~B-ڼrvoE:Ʃ3ۣK7+Y`WirS):{>ڛ}:wԨ(J_";6R%[u&ƫdZ_\'np| RJwNeTW,=rrbnkڄ[M3ܴz)3- R.?:okۼ0TU'w{6&w7j1z3ON'fGoO?)S_bQ_¿R(^ԴԴG.EtMڇ&RUiW uQjU> Kiu1d<ѥIQ'RQ1:O/lŗᏩiʂv&Jc{D5 Tt)1.n[n۶X}RjqnOʽ(~[Ns{ސ⛌uO,kgo֢dRNQȄ .'6W!׌P朼tdZjFGE"]K@'i۪N;sI[{SOzk>`rRR+!σj8&TjlvA̷Q?HyjyLHNտJMjܶT۽lG?SnKN%<‘ nq[N0Sq[Ta(&t(|HGO~gvkݻTR4&Z$#ViOY1r$6YF?e4U/Mvxų:zbU^gQQ+NW_'4jfz^c'#`rvrڡ(IJ/J ݦ6 ]-CW |_{v*_q3^DZ}Ic6Uڌ8p7{crZq5ki`)mU6|-Z5^iEz3P=:Cu7DF'k%}<C-޹ֲ̱#\,(f88%X-N(ck0VLR~} G"-8ӏ/ϰKq?(#nrVTmZ;zióM4 m |UT'C^_1X.gXM{%ʤd 4\ovN":"y-,T)fLQgۢr=/CƹǨJVr[a+!rT|%Y\ٱzsS>jͱ.oOc6f$q% ǒGo;n[];ߎjrk{~\VۓNIGn:iqxo |~t5)Rxעri{Vi&NUOl_ѮMfsޕkЄay.0P{7N((BaIP$ K"U6Gl ݙqJRu+qN$ m#*p<|{:>-Ev=86N*MM긭U*uѾ?/^o7;'u,h4݌xښRM:5.(/ \իU.{F^rmF-Jɷ.>Q"[4xT^OZ~mK}T0ݛ^SAo9u?lX(' qj%=X}"^e4wˠ|rܫ 6I\Ķ;Ӻw!'ڍWg{ i U_9Avhۣƾ+:vs/MK[ɭīe{`Zgb}r[i'GE2J7Nez579wRq+Un ]J.cJ4M:h箽Wxxm^ pc\wcN%'My $$| :$Fqɏ¾^қP9J6Wxvu}ݵP>Z'FFdg"-; [¢cmWkÎT8nG%ݣ7*\խCLRYZͤiD&J#'ehbSyXK|y*ӞpS̍R`[pTr/Eg)K+92{_ n3zwz'oŸۤ+sOj J:`T>Cf*lwd\fYOP"R E֢̔L4ɥ :;.b(B02rJ蠟9>V'9M%)IqnhP<%,r'P/vNSwr#w"ݨaqc(|{kd=^0jTMR2ULNz|.<|^PfY22##!,K~E BEJۜ&jRNsHަޛg\r,v؜.jK3)[EJ2ii{KEiHP^&]Gn8x=K}Wx/KI9-ϵwQ%spܾ[^R}S3$qvq8M[ ozKxcqmJ/ӿ{_}7&ݨ\f6ZSyQz& 7ۉ[8~UNn|nkiTB+4RI8'Nc%tn{!]Ȋo.nEmʱn𵵥J A+wy#+ikǒڂ;՛s85'KmE:Ђu""Iģ5p=БbTY-ͽڔ詻ngL2Q}$de# fs^o{DUUsfwӶ;s1T,ǤtޒQ\෼J=.tKU,7čJ5 N$y3kdSMQU~mO[03 $zAڟsF5^뜞"Կ QHmrR"ӳηer+ҔZ]hE-6Jmt'ޒ=O[sQj)6K}?e4v_KfZheޓ=BV[bY}lݒTTЬ{ȫvO_qpRApVŗ 6ju=*BR)g "O1yhb=tqJ gtm\b3RY+JQ^Ō֍\յ\>+uSi{=x ^w;uӘ#ĸzLn*$anok߷CBӷ}5Yqvdž<( "_OWit5:EZj2 B ρ1̊fi[n!HQF82q1牙nqnEpT(2RMoM4ϳOu ':֧_Xjsg jP^(ڙ{2%E͖j^}ZU[Q$'U) <܂%!s"m R'G5M0<+zM6qYm$ڕ$3ǧH]?o2N<8F1̻r_my[Rf59NjpzBnl7*{.QP 3N&^BLJPjAHCK2Q}$#~YMq8 k(MFMU)8MEqTy+Tʞ-ar5yܕOXw!e;q-Jqܶ䓊Y:LC UE{/t>r"lI9)3KJjϤA 6SEE$d߇3KG*En|P\ԭTn6I-ƍKTj<1H_zwGr19wF N8ݝ+a9ɫM6mhePi%mmD! """"""*1bRKrD"vnrM۫mmĽm]ӡiG~e"˩ lhRTMk^MX["Jݱk7_ޕ*DqĒ&flՒ}`W}~SմZ{ĕ~wm*/{{ѹ_-0ط#P]xlڱ~Tn5wi*lڪ (JxioϏbqKYR|!|KN53 OS222$jzww%i}>N)E+rۥ7c$Ofl/LNث\6H9: FY󡈾I)fB֔JI_ ֣^: 9mY{66㒢7Uj]:.-os[R&gMF3˸#໹kmjq^8W"PΦURjʄWa˧T!͋ lW48JB2ko+ /Nw QwQzQ ے%$ޓ7^YL|r7!v%Trܥ &|M8~ybrn[RV gSn{{*#2#ԽᢏӴHak" ӌcwҜw&RJ07ױ>Ļ =^ BɆ)v32.M1=#6%̠tҤnzqMwԣ~s*%-j|_m*.Yx9Sz=)qE4 3pk+,`=kNRڥ=B=nŔNAx)Q$ԩȧ4z3t#Z2lҮYn$S%y- JzGpu|LBV7ZW#;Wwipܷ%(6jFG5#{$D"uۭ~]֫SrD܃fҎӾ+Tu>-ZTQ& N|$沸ii>eRWݳu'[O̻j8JۻEѩ[]vni= ڒ,[_%kC7I3Nv$4ɎЈeٸoUu:[}Do5|zNq=Tre%ɧ6&~DȍF]ƞG5q m]/w/ \ʲr8=oʔe9U(W"|S]uZd#?Se[W"ֿh][-7Nu:T=)R}.;ml*5Dlf $fF(̏T hiIUU4Szɕ t(%_|2 ~6eM;TƗK[f&]LK^CE2[ȏBOd;Mi|cx,^6;sیGpQ\NuJIFTJ~đArh* B"$H쉩eXPRj?sl"ԥ)su]xpԴY%VESH"ЋJǰ K&5^Ukzׄ8kEgS2h&Se\ Yl]WҶp-ZUvi7QS:4byqOo+[̺腋[6-_Fo.6[7$p&^ _GZԸߍkc.qqoI[9m߸YxOZЦ1uoiSH)P9Uʄjcq= S>֙NeR><;+ڌk%_qT].srNO?s[=vH[]RZHRMtᩗVؾ:/~u)ԍdg%=edVrISb{6vSu=(ܥ)mTv/J}̇8 S3ad:^hBSf؉OɔLhI_1d8,L><_A0y3rXq"'(۱;mFNII.v5_(^q~X>y{3צ I*Vܛv/jW' T'NR'j%ꔩ:mJ3SB}΋!-H-RJBТQoedi9tjENenPpke.%4]#{:>mkEɱdYWl\\\'nRM4&U>?Ќˉk÷!𴪛]]5}UqG~ݏI"O~s6(Ļ)qO~h}uԕd}Q~G,oE!&G&/]_H-O=o{k\̭bkv.Ô܈+;arZx)m?M\3lU$mk-CFXjTv6u' g:Vn_*qk:VC A%'4JV%EY)#BғO4<e׿jQQ]yUr4=wm[K1r׵%Iũ-O}|kC;/VcݩWZ)EHdžTru]8hgĵ-;=>U_ InvTm_jBM+QiF"9*{DI/iuo(=TzϖmPQl_v4z>T*ȴ>YF;ε\t]EH4ꌇ[VrLzef 2T^V>g2~kg5~Nק;{~Z~W}&ŒBӿS2$J?~(Yœ"˲ߩ\O]: J׉ښT{mmIѩn3˧)4LdFZ/zUG>U> n 5& ϴ-KJi2o]uKljvK3$bԔҚV旧iY5.ίfi96v7!v))FJM4{jG~Jt/lUE%pTAFe4qQk\ve۽/u/Im+W')v{\-E|Pms7߮DZRr۞/mu*1ՙaB܆ -xg3#6ۥtRogʌU)׎]ZҞNnŞr}F1Nnޞ;cZ{N}ۿMiuxʉ*3qi'9KHQ$WJxXyرŔe~[v5~/jN9Q4o6rJv FrdxM*iRjMzUinHdн7ᾞS=S'7 } ̽zt7K|_g J=Lq+/Bw_\ۧx\HJUPzQ<hqF[V0x==CsU7q|^ {)Iq38$_A(VgcKu06Ƅ"%i~_ˉk QCܣB8Ku/񋇵u([w}$F|8TՠI.E !;RJ^}MɒD_q2];Ɖ{5}*n7nEInO{Mwv}&q+v [V}Ĝ@%>#dXQ$f;iep.GquixVt x6bj͵mlKقQ[T]zs/&yەnM'W}!Fp_d^Tu N{ɻ'l{խ2.sTu{W^H&;1s)Pӛ6>$mě;Łnj= fLT)>׸+qReɴ[UR\L*P/!$Ӊ3Q 'K=m~6XqW3^W+ųO_[F$rR*u"T%@O +%# ]˽!aܽz{ͷvQh쩎]hGތ5ɇ*DzJDRNLi 4:{~2FmXY-zzĽ^f=]uū{/+&c:Ma{ĝDp2m܍kHș/(--m_vݮK(V{R}.k&yƴ7i^4@3f sK3^Ř˸B=]?gt5KbZB<e;kQLpxuWC}n 5ҴepB##~q= `x]KWF {GfŲ}?G.I9pjWkU]>={7q{kO/^I3==f1ɏ%nnʫ/Zu_yXN<57ۍ'vy/"8넭M2eԷ&Y,в33%IkjMr7xf nmQkX4踼>a-GcIeތw&U=-:qnW)z¥j :WqSZvԒ#j"KrIU)%qrmRoDGQ~SYRsu*V)  ,/x)MFD6O#]z 96[Ui(JRfw'y$GeUީkdMF-ݻ98F2d[o{Rn0n-xsV6Dh|Eb2E:KCOӪv4SJCr"J!!m,hRLD| ZYFm/X~ΧfrN&4Ƒ=Z9Mh.Mܵw/BdrܥniŪ8ɧ|y%œ[M=_tj?F!z5\evM:\ ~F-sg钬OWq“iiȍ<Gi%%n2rqͻllƑ)okw7}\Uk-:&fj솘XerV9yZuʼşdFC=rmo%~ZN78X(N)_7.Εn1MpJ}62jjJdI";R5&iLԸc:jmqiQj$ujp\{;v5B񥍪Xn Ą4qOERjzN(Ga٠䌡)p*v(J7#ZۻZ8O W uONb+^Qipv9GvֽƼϯrYƖKGJQDNPhRJjᡧC"21"9ѓS1;R_O7/WGz)8fE%F2ukmvSov/iZ&/]~KmI[:^~ͤ\kMi稜\ywJt3W7 8Ʒ~ݥeFgѼw"8VVSج\뻆}ݭ/J6Q)d|)zU3>k\L=;ow֯gN3pKѫ|wmkZ$z^2R:E)f>ς нd|#׆?\ǔpV{;\$ƵE%-ͪm0S6[n< kE[}mvE4DDZ^$OZ0*$~XUv҅B@^?]so#%ojw;Y#SxxueBگy v^i-)s)zV jC{7Gt.w3v,ygg8s]aE_,*E tY5k٨h=o"m泏:\6w噓aiL׎n^c\75AGkЯ0Lf46َ`egZ˓p/k;̛]kq!ݸzpԭG"}R9Ve>ˏHUjJ-&7nrnwG*Xv\˱/vN}O)ʼn&CV͍f̵]r\PMB-6Du-#RͰtRN^)mT _}nSȕC*_xBuTkJW[`ɩ`ejvsngP ڻ.-WUtܑqԹQj)t;vN&RNũT+8%IXӃ5fK՛-d9 ]CƑm|nZ-6=Hz,*aEm W3VzRšdY~Xf׀Xx"]s;)5u*ُHB BRGS6bݶؿ 9j[1*jױga7oX CUI%0v#~\-O-Ꙛuɷ쏪&5mY٦M`LJ2qK~HZbr =N'YobI. (^ ׾{_ ?OJ`S`3BN[}5w6:ǵ/iSlt=4F*d&T4y/#. ɵim5Uֲf 眕6Y7 fơ=3dϕq뚩$qTM-%r!$@A? ޾V0c~{[{;򥧅a~ڵ»&ڄv1ek=wb MLkNAԬw-x>~/r=e73VeVN)K%Sښe"+3uXuچrn ֺVzscJ峻m}vb㶓n\YbIUBT%*,0nov=;z꣓S/nSXSpl##k9mXGrZv^Gde!ŷRԠzQyjC]`gToPov{j~KRBMY}i[߶9KL2ԉO0K#m>wB[ٍ+n[[b٦DX ݲpo] [\m5qdT()mo4Oy9Ie b][wղmM~vmi۱~t \}$яimRk(L c Cvk7r9_r1 ;zv|F@KyZ[&jEji/"6$69ml#e]9s\{ScL}Ȣؿ0q/nZ*t,CLoD߉Njǚy=Pgmu6^]l-["çUʖMlʍp-"qmU>۷uFOJ%Ǔkx 'g=睋k[3u,{³WɘݪF]ՍeFX"Oy\,cچ=w/gn Ļ]#2? vqy-gXnR.^}ݺFs{ŝG]}e|#0mjx"ƬWكm?rgU^xVB":Dt>@LRbun~ݭ,w+v⪕;\U(RYa61>#Jm˞Μ9g9XKaG='u8gf}'qy#ɉw J]We.ʲ-<+&q%s?2dњztҼn`cΤmmqMdz O[-ߩӲ&;[tmܝVnr">{x<8U+p:Ig]zjGkt,uzf}dؠoJaکqEq -(:d<պ=eKy[˗^%ZXkX[C2߱\ITTLGzANM￵i]K>UsOGDDD.ZF6* ҃V Zhz{'xp^`wo8r0h ZmJ5"jb[l=yUu7-;7IT%:jFjߖm0tzU'K)څNۧYJ)4IQ}^KWm7kSP>q;ނ#)'n7&׊r?óM{IwR\j2Qn[v pe#/tAF\ϵ225q֒om6z})6҅*oqDsMf CNIN=T S2t,_ѧ}kveMF0J\Rnnݙܹy[rUc-j{yGtkQ%s]5qB.Nw.JN1LvR Ui5J ZESQԙr):MJ+g}χ!2;q([jAud][ljVK3$ײSJI=/|&tl'*n۽f.frܥ jQO8>&Z];.|7T/C}$ڋUmP2Reҭ8hFF\L 3~e v\۫]ݝNmrnB%*]Z«hKc=BTLG :V74$=Ǘy+EX'4tn(I:Ѝ;Df8c,k1%dJ6.j6ź{N~l6&*fœI7 WAlGOu-ҢH,,(ǔe뿋쩨kM܍ZſgRvQ' 9)?n|er˭|I|-fGK.rΛp8XV1%K6mvG+tc+qE&ǸC_Nm:l=_/m5^[dߌڇ.c<%:)tQ$Ow~-aY;UJ>=F)2[nk؆?훐M=l6[4(O.]2#-H^n#->&mp5~Fӛ+|| S,xag%qkEUzUgæBhߕP(7]kFnq?֖CpruZ6*rEڊtS|*tI*E}7R<,nUU֫^I7Q*mSly%rdȓd8hE<9oHhMfNSRj[i7D[Rj݊+kდq{"$$H?p\̅S?㭻;t~R߁)^/>Qj`yt[w ԛ;²~+ߔ_ YW~|o]?x^ᯛ `ʼn;g)T@vWn]>&4lp+$D̢1l|ȨF%-}.9[}w~ ԠLM9hСablfe&QoW!s?wjLK?s7yO>(=C~_nyǜu?v3vyo oI@qV-jeES^[9WoSܝh"l2C1a͔CiJ@3:Pճw=/7ovuk+\V;lDgն<[A+rX~d;m!_s8ݖ׷;;.0llUC+?i#_crʙ1~C.\–q ul8Hܶ2m`ܻM3Tov|Bs rɵ"oLS- DКw=Tv@f'6|YlD͓Y%׵-#Ѯo%:&!3o%\J<02;K87>^vgƓ# ;ݝmz^Y6=PS39U%~ &f# }o!muH;ʲŇ˷yvP+&.7e[3'vR4Yj̗IZ`e˽3o[WU{ m[sUbۋZǾۆl6~9'V*.\S2<Sd*zY[aŶ`]C$n.v^Ʌ dng>ەZ,Mmϑ :n6nϦezWqUJ4! ۇ4R! =>>Fn|Q[{pRO17ƕ~._I''00k=b՛o}Osðc2'o\3}ݭQ^2 . R1yKȣtAݿ-uܾw!`?1Whn|gzUo[ECWwjUIן)^h#1ɭ!/Z np;o;ΗŻkXs."6E`Z1 עӐ9Kl8qd q} 2Stt;#j>;խabONŗ=fwP1j)l6J̶|gV2`y/0E˛6+ԫ1? 6}KW c\KoKͨ2ۅFw–s*TԞLיuDx .kCzWXhy۶gLu|%TnupǺl-S* PRaLnT+c+*xl.v!.U=|; !_L̎뱚U=4hm:ٯ"y)$:>%(n}X'p[ȴ ^˒4kƓmzDx \ 'NqamP7nyN݅=j7%McSڵj%STy qXymvCg{w/w=wSW5r̹u erծˊsOm=DhEҚRb#n)QOxtվQwe]I}wCa'"[ۂ-z}2UuKP$㜉ԧ:mc<Ý>RoL?wu|%ҷ&K y_!y9 ??:tq3(UU-lkS'ɸ@jdzQˬR] EVPW1DJq2n:,c|ǻ̑;y{X,ۂ.u.b˕u.tKBjQ"[S園S`ٮdNبeJ&9Ơ ~0a(Vm٘L+Jr*vڑE( x0+tp˕ n';wm-ޜMOxX>{#2%jgb2M[`K*\5@8l'e=0u+w ֘鳾{y܀:R*Ya]"Ӧ%ktynlۣ65,3gU}{GYrb;ge'TKwǘ.,rpܚV]Tr,!dp /ԺU,xՉ>s׽~W5oTh yx?xrrx?)?ilbT׬,z$Ԏ.UH٠\U1pU:]JwSrGZq8àd驐,N67QYBӢD㏙W!Q25ϸo9ms-7-%3CihO.J鯽-;MZM8ku-7k9S$8]q2E(}bۏI[DKOK}3KUB^u %Y,u.-&f#]'܆o$x`Yu,dzwM;#oKxn;\[d7}Rb+*Y䛂ZuBӱl{j0O̓}LhK;[aֶaGL{Cb#S.T[>߃F]NK"u^LUʐ_ykW?!GRj29͖qa'0[npcDvV)qz9R)PۨM^aJx W] r>];eN3vxdmĘ(5W2K1䪖weF{mE/QP6\u54x5[hۮ-Nk”i[lUgL]J}5 S:EhiUrgHl!ŒJ$pe=q^b͵Q' ?6|R\,JA ڵ"TDꈭ:ymg`B5t%M] <N_zv2_Ortٵ/i/ReӮ*7[qүqEG* m"[I:6e^p"I$jԴęh!m)]GZkcjS!{e^z}+Cѥ9;R|/ֱeiUԏCNu2Zhcٗg$ݭwvr P8*7/Lk~I'Km1+MW%Bk|oOm>-#qj*|Dbѱkn|n{v#jĮqNpMIUm(7Liz;{ҜݞڝVƚVϬ+sO!OstGvxӉ']uӎ4g_ 1^-8ۦ k!)Ύ5O;YSB#2Zzχ;<.ֵOtge~.(RC#wFZeGZٸ6FFJ4e2ˇpJT$[wgV)q6muDGJ56q\I!̗ y/I~RtJ9kJ]Iy*'FN0s.[l!fw'y(7$œ WƫgyΙdMEU JQJv̋vmrۖ.jWR_M֨djYgSj0^\y'EoECjm$ IƩK>Z28J2TiJ2N#}.s cArl嫶nB.FIJ.)۔\ZiM>/hLĸ=C1s[?YMqp|94- 鮝𦔽/k^#NT(Y LS$6˩}{;5 )B۷W$qpN)qqoot}ZDVә;7TiK|6f3h$dԄ}fqݡ>Nb򗉉+ͶO]>ߡ_VtYf79ڰիF sq~prս|QM)g%l0ocJȨHz V;Bb/kLAcfPJ,ԭ{ƍgpjNR6VSI*$!yV足jᇑ.](EܣqM\qJ2eZT).<9UB/(B0j)mtKEj#׿fDI-=rZړj|'Nڤ]k*i$5qt"ݙPM6E4ke^Z8ۏhz$Q(R Ay2zfRñnpnkbkI:=j &ΝșW?׵d{+ύM'??XqeeĽ.[o=UxFS=ӷdZwenՄ]_X=ĭVa* pKs0ބۍfJ3 gz̚i|wnxtjc¼5${(1fXQ65ȼb̶Zkn>%FQMJXӡ{TZEVNᖣimT/37cNJUPnP҂ZOE~"-Rc4^b- FEͧtf5[)S!OZIښݲ͑;tvܡ+N)AR=hCNn;wL16-:特7M$=Tҕ-.R[HٷnXk sn[ҞD-0WS9p9:-Ϸ-jѬNu{ҹfv)[Ľvwfg(ٷfe+0mYj8Q1\ݧg]Eǎvڿc!4#j5̋C2"}BRriFp7=ô\TZ:\BLfj#I22װ<;صZl j 6:l"6]۸ K'6RTѯ^ئOԓV\?$x7s#r:Oh{ց=MmuHԷd{pN /܅:UE#Yy+(SgQ(Щ)RHzw>^Ѿݻ>mK&^ '$Jۻ&w%F|xfz%˳ L~3N?Cy9 v w/{ƿ kz3x> sXv}vP"@WyC z`'톽Dw%-tt yVY\wmuPYQA0iG-2JP,6/gˢ]u.-n!Zw.N7Q]Df}Q0({a\@=i_X7gFǘ8^⻲}G MZ1)WEfO12G+=-B@z\`||w6ċj߬m}UwRox֢I &c~XGP6Qndpvܻul'V7^FJt^{b^B(L~sѣ6@߿^xqU!ڙ5|Vpvef-uӥ^3  FSDɯKD%0r}FF穛r7 +o"V8tv̖NQU!5uFd"bCr^bJ=֤fM#ʳԷP0O-9xRBm\=`r-:;~3Tl(nXtXi%2Vٛ#vwqƴ`L@"H‹qW.j,JM5B[)WܺUeZFqc'V˷1W7V̾-MHФwn8N;HPSdݷC7&2j.W\τGŎ'Vb]c.x+Rx1%C2T{myg[qU|+m:M:շ8҉yWd)ՋWS%%:iqlʹmGwݹ WnNŤѩ5(9hTٵDdGUi-)vSs2 2{OnT$Xck n:¶(lASLeȔBjμPpTb2~N2~%^k[ܗ[Jzs0ӓHBKq[}JَA-$dFQgjxxFv4r/x*Rm% `4J(&iv7SkԲmSH1YWmx 8n.k']:Z˭_W >ڃXЩ. jTq%Aā[E}amc]D:rmHRiu:uӚӢ\p(5-q%e)(۬ҖȽIf<߽pr&ݫVfY91q2ĭEQgYbTGQ&,yL+N$[q*RVۉQ=FuTܻ>f>f㋳8N6$܌n)9&»iˤsX,݅܍ȩv+sRTpO}d?Wn/Inpȸ%O]StQO|v5\}7Zwb.AIVK^:wb{[uݯcytO߶S<{8KSRׁH̏N7ۚ[xkwYy_'ZӵF+>쌛ZUĦreE9F[24De{}@:ExWs-\ǻ7K-\JNvEk%:s˙#κ].oͳ;լ7wB6nwu:$L; DkI#Wz.:Xp(˅v$Sq,wn\qIN-e<5Oe+vuYTpcojUI_ާP8 O 7&VL8z$_B-H-[uh]T{|8=qVRN-:Ij:7PUtXϷmy鉿:RIM~33ӸS2#׳GdŲ5+/Bx{(WzȨ5Y㞎#|˖+ ط.|e<o/rߔX>7s}VE.OVti׽ .5nNJO"95{#q}Ay9do]R"M6z\tnNS-D!@3N_jicWsy*5uٮRcWv/.,j}=S)j5C^> Ie =gu9ӛqjtz]۪TMoߧI!Ǧ¶m:,"[L!{qAv-o 3{"KʼnrIkfٶj2ƙ؄S`7` k6jzޞ?e5G&6uʷ2%ԒRKE*G\Npom F/V |C0.q_eenƣ<5Oh'67ɪn[SĽ{ڔjǘzs;~׌(ۂ`ܢ1ƣ` _l9Va6%UQWh~P~\F^ZHR@:ۧCJ{ôGeBh;~ۧnU J\O+n2 RҠ)ng}Kh{5+S×ܛ.1ZjG)iRȤIN 4%{oΜ/eO[Nffd ĹK?nnԼMqX'܌nZvq<ķbFnͪaQ`5 s,M_լ?-@_{w{ӺձJ}GF[%v\5[ŒGkOw/ΜM9rjË%2+rd~+󲕛C9U۳r[aJǭm|˒LAʨSCq[XMۺoubfp:t+ΤĻo ][ zt-*67kvS7D·MMCQXm;)܎n_h%]4ܙnRk!]ڵsDUF"`R, &#R_*[z*ZqFXɻ]7|۵w+'pFDەs=r./ᐚm3Hשy yD"jHCr':sA65نѮ^o1V/ f;nFr3VM)e*- s D'H݅fӧ\*޷[k<7u<-]֍Q8R h|p=WlW3s%Q %3l}@U-K6f-NϿu|ڴmWN׮[׸F*mW\%r! C78:޳vBG7ŵ.JթԚ2x)ST!řn~9 W:Wpܢ件{xf8ٳwKE ҰWxVB\qBZ 2wMb[lGSnyԚ~z9ZmያvoN2Afnݽjf>)j3 !;gOYʹK" Wftڎ+׭b*2ϻK>ۢӱeyԪXISUm[z+ugX%0lϏnvg!;t{BqPj>PyvR7Cj]O%+ݲ :qiMj6W}3vC/R=4Som]ŗ=ю, TF6U_-\6MyskwMr&Q\wjKܩyMϣUj0*}RZܷSdY3>Zjqj6TgzpA/M`/Cmл,޻feE[/+uk^Vs1W$G(JsW2ٰu*߻q*Y޵.Wi:ur5T),=0uRmho.twܖiYwrWHntvEj8qhf`Ͻpf(R&>Ki%I7$QӖm-2 ~yߗQ-앑/ x[k8nw.c㩵k}]FkbJl:{.(˩n0Hqvαp7 귎.Gupx[N`Yq'+ruU7[ү+>!xrȫoSo]OC# d^Q]\>!ƛGw^Mx"-+%vdX-:M2UR%d>%l ioSu6lsj7D P>XxHz Ukà(n^Q V>5cVtWj SEiJdznyej[lE' 3kuٌNn4JW)gB {4 j6&]' m-(ZMEz8cz>WZ6#7+[,MR-Z!4ܓtCyE|umj1ƽvƷV\;%>Q :#Le(iVz5 4ũۤUWxX ^(ҔsլB2w-V ^R+; ˂M\z+Uwr+RWY⺧~ Q*JcYSNSλUd8in=v K낫k\IRרSUaCFmϿ5̗P|u ZTԕ}>oYѲ1sfP+sQkX8Gb~6r,s>^\,mGL+7[n-E\.Fqḕcl*Jmjb5 ,m]c}NXfeVlǸJ5eˡ$4%g~N p4Y*WwW٧<8v#;qԩTut,m"#Y D\5V`\\Lȋ];LȇiS6ϝZ l>LruR\v=ǘϔDg=ԈdFZ+M{=|,[;0>RiSi4,S5}yxw&(E7&fݙ4UՕ! ~'Id)]ǽu2K-fޭ \08Vڅ쓬=Vy^^ IhyKR-B#Ըr=]mܻӾ'*Umkoy rTqT_i,/8Q^<ݤ|4ԻO(܄"'5N~#m.(Ҿ2i6Uev&I*<}҄$eNtÛzyWJubW^iBW.܅Wڮg]irO6Ve90sgv.+sV޿aޔ[p?3q*FutUo*eL\KM'EG*ZcAFfG5J 5jj=MJ3OK:k˝'NMB7m3uFҕ\-Ywg%PRqMIyZGY9|μvn߻5cWݷa^+X֥vnݘ\v7m>Fgzv"-;Ew֝}1|RjN𿊀7g#֟*GQQ|#/bo]p$>_Un9гUbn9׃ErQBU-^vDmVh'<R[fdHT]*~}3j;nvjc7s-rӳ Y8[n[1pJx kX[Jk9Mn!_Nю6x:iZ˦U |߉^Ԛ݃hYxk &U^bwKk.[jE+P(˞=9j@snCv7%c_7=xǁ<l {t'酚+1F‹l׭:ݻILruǶkL-L(K0L1&>wXB(pm;1fpnlp֓%Skidkt(U +xulo'/ڕeN r=^pZZ:Pnj8Hf"48ijY[ N[yZٻ+=  ø:3 ?^ܷ^Sr#YK[UF?CuhC b]GM')mڏsNrܗI]ljq6VB. W,UK"YX5{c >Iqā> T:n!,5l2VzCl|+I[*SrjnS6٨y+x,@>П.g+!rn9>N|W>OZT_ut Y""v7|sfި;Pclm EùN,{'fNT%U&LfH8~1v>Il}统u6P˗c(WV~H^bMU.o*oOF0N:_:6Smr_.b+|ݶYY غF,mwjv>f*>QM뭱Sd:`N{l/⎱;n-z~"Gze퇎J5S KG9!Gn;N1 ݎ h6m|S?ɂ5'WOÞ 7|7^ao @mxGmi^jϽ>01Mf0լD3-2T. VXR"ɥV Kl J O7|u?bvа;6.eߓ|[1bmRr,eRz`z 6܎-ͨku͹Fː dPhYgZUj}nvX;z=gVեTv_J }\1n7w2J?ޘγc\E 1Aޑzq;\r]]\Y&[nsNei\uURje*Qk2CSl*xJz-xٶlm+|UjUؓ`Ladqiĩ!Gd\W~fz;Tn*PdRM&T4`չSWq5k훶(N"Ӎ% V]֦wb.nUO!u*J&Oӕ2e|Z=eV쫚΅g#+/RW:طnbi*Wyo)p{:ETKؚR(RY+r웓r(IF) VmȵNB:h Q1ғ|u8E]{,'$-TR[j49l*3"I鯴zhd>Q+\BkNF=.$ZR4Nwհ(IpNi.(Gi33#33e$FXK*NdWrud[r{xnk$v2ıh+J1TQ[#JQl[tRO]LHKٮ NӍnF񨔤֞Em'MILB"ԋ%dBŋ+p̿_17jzT~4pc Vo\ƹb9Rq-'1j;8ܗ)hE%DZKS<璸Bu*%*Yw5ڻ9ۣ^z4U; Ñk\U(o~G?VUĎ:?P?_F_Kߤ~ᓾI |pr.Ok\SklRhҪz{­P .}SktZ7UQ4ڌIM8̈eaӊJZ%FFZu,KZvln廐SNFIVtuNi?CM5]+Ph,{jN JSR$IS^tSUVrORYu.9WyP6 [Kiu m!X|]Y79ӄ)\ģ)pbڳr%*&ꑶ_-H*dzk)1 V3')UAϹٶWRxe'պn۫h7AR9 EAJeGLms!%D| A 5]/Q3eb̄vnVn%za\m kZnv([emqrIҕij|""><hjJשvvǕ|Pޟs}V~2&Z?+2N&Z4w@)4iSڪ_>/JN9Hiۏuf8'It[ȲR.hZ$ȋ_Y ~U<UUO*6b)Ovzڜj\R̋.$FsQuҊj^נ䈈y<zZIuP[}Qm=C?zN(Exqu/kn S-FzKZzOסӽjJ\)F3b!r5ٝ|;6 o=-3*λ]αb\abqRi-w޵⦪~b8Kpo)Z=>)ғ"5/GTZLE-輵f7ݘ۹~+&+w/7GFI:l33fg.N~۲\2|*cnermnnM+Fq"ѪIz%j =YW8@~gc/~?N'?)«qȸs➟n=k" X“m֮VreMh2[uݖ] *FܖN)MȐ`f0 g,C9̑o;ddudJ=In13:ݒvvdMUEJLp^,6t-@͐9'{7m{-3,>hnF;ѰM)->>+Ěz!R* :`e--m7nB\u{b U>[8֪]6^ߤLʦ\DFNo$$dͶlgno8OrsQ\l̯hRo8tuNo+ CTxu!2[>ctFpeޓƻֶR"3QrQuOѳgwQr;S~)6HhZw/GgVTmUf_yt7%$];zLWF̰xy2Ʉu!MCmš_0[W6jf#a-KLi+3Q7c^qg%s<1aYIQeZf+}>;S6L0]Yu_h9߻<ƅpmiM$AVvŚ,*#t2.8Y)-Zhshü97/#Oro"u^/uFgWɺ,p:6a,^x%$Yve^3PƗMnTP&yS}OJ '덫MH^:rXԴJۋ/rI;S*,+yz1hv)Qw^ڍJ2oL׊q(\fDj:^T%vOadɂnS}ZO)N*λdaȜkG_PIEO}нa(^iQX᯦-7^)%g'SJx(.S9zVɴZ{E ))ۅi/s7 VIV-|sj0*UBTHIqRf>FP$KqN0 R̻8j\GcC}IUz\i 6F)Q{Gҧ3qSzKj-Az VЛS-zy:8*mNk|D鿓ND2u+0Yŝ7kqm·?8Ib]u>˗^_>(]vӋzv+ݩ){vZrJ2RQ몋C$z [,pp,8mڊbR]Il .f~d/ݓs㓓mͶ{mgjQwn=Oic9ܚm4Q/6ݨ[TƧ?nԶoytf{@AzT{e{[O'ZRZt~AGD?s3􌿂ՉIw'|~U\ w~di:Kޱ)U/sU%njѩ&GSP^ǝd)..!^U` 1wX[aԇSxoFV6_扐)T 2Mfd=ۖͭiZ7KK Bi9%7@<3<ճԻU,},a}FRqɛr i@ONJvK KLN M, ʖv0n-]DwlI-X6ܶ$Jʴh5O+mOI+Ra瞠\ MG7BفjYo1#͖0V`Ѱ2M?c8>-Crt*JkIGS:e#hPKx[鱼>{5m;wcն&>j-M֥^َ) 6yȜl_w{-ō̱r> U=]iw3)r*]:K]6BdCTZ|>gf}LW}[$'Y5 &c -j.z6R 67MԷFMnÌwI7w5E}o޽+K ֵy4܌ȥW"COyR[q5Ӱ͙f[v"_#q{MV6܍3"u9BK(41ӯqˇc${ߝCi6I(OmθzҜ5k^:>Jzw.>qV8{vU[ڶEm|DžBz].KHjI]x;Mɗ{m,qZXr忇2u^RO2Z}ZێS[2Jen!*NDcrBUً4<ǼMҲs1Zw57c3&ĖڻzmP*FuJG1-dN:|OU}ҵgi2t~F^^Z.VxjvŧnNNh<:]^~NN+ge^g.SԔGFe߯'[vn'(ScJ]kܗ7eJOlRrfziݮq̋S"\*U<*W]k$FջV}? 7g#֟*GQQ|#/bo]p$>_Un9;l S VvQU%OLU{οmU6bZ1MTx%!֙Q7, J=!3 ;Q,ڌ;6ͱ݅q^&ߔ·n #WbwӖX.HtG)N&d̵zpI,n cu ޖUj+VXUp[w]N o.J6Z8Ts&utxln;~HPHS/xw`G\ʡ¿rj Z^vt"[L:SD\h0sUwR,}[x^X,R2Vn< ]2YDr[SRKs8tXb̷G?Ps Tv 3be,zVz D[/I.KOEQrm'$7|[J>r S`5յwT#\w1FTz\Ԛ &"ׅhSHrD\'r]~/>p;:Piuu:"9ő=tTaS7V2rӷk7mb[^WmPp*[y.Þ6f]cizJCgRR@UVl큝.WJP1N{/\whZ ػϧӱE7|E֫Sί.x-Y&pi%v''-x6r'Ws*6=DwwUu]=C?MK [yrtܒG$!WGqJ*%SAz ED[^)/tė/g=#Omd.|^n/sl׉g DZqemqowݮRzUܜ=ڽ-o/Iۖ;qVʘgPp|mm;6zGl9.8pwWgsJ2qPbe}}UpNjٯ}7TMQKrؽtEx%v w߾8%|j;~|}pK]ơ/ w߾8%|j;~|}pK]ơ/ w&~e_H 8PL7:%ʭ5Kw&U2vwR_+rm'}C7#rWoO&HoG?M$UR7{FU]u ;# !Wk`|W>׹潇9Vn)6)*ҹ{%qV4q>W1vi#T"Qk&GwxcJBJ- Ϸ^ˁxkU}ԣ/3.;]J=<*)cS)ROK9H=,r zX @)cS)Da^ԽQ gxJI=w֣gf*TRj

Corresponding author (ishikawa@ems.okayama-u.ac.jp)
• Received: October 9, 2008   • Revised: January 26, 2009   • Accepted: January 27, 2009

Copyright © 2009 by The Korean Society for Parasitology

  • 10,313 Views
  • 126 Download
  • 7 Crossref
next

Full Article

Download PDF Download PDF
  • A mathematical model for transmission of schistosomes is useful to predict effects of various control measures on suppression of these parasites. This review focuses on epidemiological and environmental factors in Schistosoma japonicum and Schistosoma mekongi infections and recent advances in mathematical models of Schistosoma transmission.
  • Key words: Schistosoma japonicum, Schistosoma mekongi, mathematical model, control strategies
Schistosomiasis is an important disease problem in several Asian countries. Schistosomiasis japonica is prevalent in China and the Philippines, where millions of people are affected. Schistosomiasis mekongi is prevalent in the Mekong River basin (MRB) from the Khong district in southern Laos to Kratie province in northern Cambodia. The total population at risk for schistosomiasis mekongi is estimated to be 60,000 in Laos and 80,000 in Cambodia [1]. The first human case of Schistosoma mekongi infection was reported as Schistosoma japonicum infection in 1957 [2]. Afterwards, S. mekongi was identified as a new species of Schistosoma [3]. S. japonicum and S. mekongi have a complicated mode of transmission. As part of the life cycle occurs in the environment outside of the host, it is difficult to measure the transmission rate on the basis of field observations [4]. Therefore, a mathematical model for Schistosoma transmission could be useful for estimating its prevalence, and model simulations can be instrumental in managing various control strategies. There have been many studies involving the mathematical modeling of transmission for S. japonicum since 1965 [4-12], while there have been only 2 studies on mathematical modeling of the transmission of S. mekongi [13,14]. This review focuses on the epidemiological and environmental factors in S. japonicum and S. mekongi infections and the recent advances in mathematical models of Schistosoma transmission.
S. japonicum and S. mekongi carry out their transmission cycle in definitive and intermediate hosts. Humans are the major definitive hosts, and many domestic and wild mammals were found to be reservoirs [15-19], whereas the intermediate hosts are only snails. Cercariae, which are released from infected snails, penetrate into the definitive host via the skin and develop into mature adults in the host; female adults produce eggs throughout their life-span. A mathematical model that quantitatively describes Schistosoma transmission needs to include the following components [4,14].

  1. Dynamics of the human population and behavior of humans related to water contact

  2. Dynamics of the intermediate host population

  3. Fluctuation of water level in the Mekong River (only for S. mekongi)

  4. Contribution of animal reservoirs

  5. Effect of control measures

Oncomelania spp. snails were recognized as intermediate hosts of S. japonicum; O. quadrasi and O. hupensis were identified in the Philippines [20,21] and in China [16], respectively. As snail density varies according to time and circumstances, it is difficult to make accurate estimates of snail density. In Bohol, the Philippines, a water area fluctuates seasonally according to rainfalls [4]. In regard to the longevity of snails, the mortality rate among infected snails is higher than that among uninfected snails [20,22].
Neotricula aperta is recognized as the intermediate host of S. mekongi, which is composed of 3 races (α, β, and γ). Races α and γ range in the MRB from Khong to Kratie, whereas race β lives in the Mun River, a tributary of the Mekong River [23]. Race γ shows the highest susceptibility to miracidia among the 3 races [24].
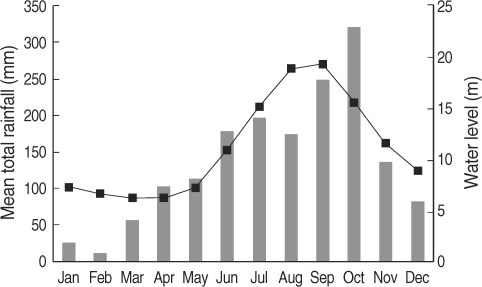
In Cambodia, the rainy season begins in March, and heavy rainfall lasts from June to October; the rainfall drops dramatically in November, and thereafter the dry season lasts from December to February. The heavy rainfall and the arrival of the dry season results in rising and dropping water levels in the Mekong River (World Weather Information Service; Mekong River Commission) (Fig. 1). 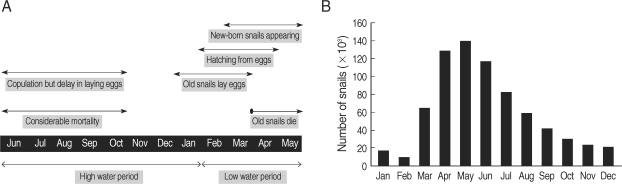The biology of N. aperta is still largely unknown because of the impracticality of field observations during the high water period of the Mekong River. The "Post-Spate Survival" hypothesis that N. aperta survive and copulate during the high water period of the Mekong River, but that laying eggs could be delayed until next January, and that thereafter the eggs hatch from February has been used to represent the population dynamics of N. aperta [14,25] (Fig. 2).
When animal reservoirs play a part in the reproduction of Schistosoma, it is necessary to give careful consideration to them because of the difficulty in eliminating Schistosoma by means of chemotherapy for humans only [26]. In Lyte, the Philippines, many domestic animals such as dogs, pigs, and cows were found to be reservoirs for S. japonicum [15], while in Bohol, the Philippines, only rats were infected by S. japonicum with a low prevalence rate from the results of field surveys [21]. In China, more than 40 species of domestic and wild mammalians have been identified as reservoirs for S. japonicum [16]. In the MRB, dogs and pigs have been recognized as reservoirs for S. mekongi [18,19]. In Laos, the prevalence in dogs was estimated as 11% [18] and 29.2% [17].
Macdonald [5] first proposed a mathematical model for Schistosoma transmission, and thereafter a number of mathematical models for Schistosoma transmission have been published, mainly from the theoretical point of view [5-8]. Anderson and May [22] studied the prevalence of snail infection based on empirical evidence. A stochastic model for schistosomiasis developed from a model for onchocerciasis aimed to evaluate control strategies [9]. A series of studies on modeling of S. japonicum transmission and control in China have been performed [10-12]. Ishikawa et al. [4] developed a model of S. japonicum transmission that took account of seasonal variations in snail density, animal reservoirs, rats, and high and low cercarial shedding stages in snails to predict the effects of control measures against S. japonicum in Bohol, the Philippines (Fig. 3). A couple of studies proposed a mathematical model for the transmission of S. mekongi in Cambodia with age-structure, which was aimed at estimating the coverage rate and range of ages in targeted mass treatment (TT) to interrupt Schistosoma transmission [13,14]. The fluctuation of water level in the Mekong River, dynamics of the intermediate snail host population, and the contribution of an animal reservoir, dogs, were incorporated into this model [14].
A collaborative project of the Schistosomiasis Control Service of the Philippine Department of Health and the Sasakawa Memorial Health Foundation of Japan has been continuing since 1981 in Bohol [21]. The major approach to the control of S. japonicum consists of 2 methods: the detection of infected individuals and chemotherapeutic treatment, snail control by environmental changes such as land reclamation and cement lining of ditches, and using molluscicides. The comparative simulations showed that the prevalence in inhabitants and the density of infected snails could be restored swiftly after the completion of 4 courses of yearly selected mass treatments without snail control, that the prevalence in inhabitants could be reduced gradually by snail control measures alone, and that the prevalence in inhabitants and the density of infected snails would be eliminated by human control together with snail control [4] (Fig. 4).
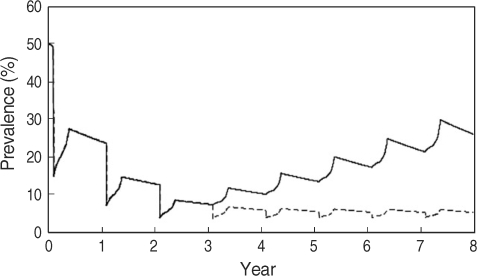
In the MRB, snail control measures such as using molluscicides are ineffective because of the Mekong River flow rate. In Cambodia, a universal treatment campaign (UT) was initiated by the Cambodian government, WHO, and Medecine Sans Frontieres in 1995. The Sasakawa Memorial Health Foundation has rendered support for control of schistosomiasis mekongi since 1997. In Laos, although the average prevalence of schistosomiasis mekongi decreased to less than 1% after mass treatment with praziquantel during a 10-year control program [27], a resurgence of schistosomiasis in the Khong district was confirmed by epidemiological surveys by WHO in 2003 [28]. Comparative simulations for the situation of an interruption in mass treatments after 3 courses of yearly UT showed that the prevalence in inhabitants increased swiftly, while the effect of yearly TT for children of 5-19 years old, who show higher prevalence and intensity of infection, after 3 courses of yearly UT would keep the prevalence in inhabitants low throughout an 8-year simulation [14] (Fig. 5).
Recent advances in mathematical modeling of the transmission of S. japonicum and S. mekongi are summarized here. There has been steady progress in the mathematical modeling of Schistosoma transmission taking into consideration of the ecology of snails and the behavior of inhabitants. The model simulations suggested that, among various possible control measures, a selective mass treatment program coordinated with snail control would be effective for the elimination of S. japonicum. The model simulations also predicted that the suppression of schistosomiasis mekongi could be possible in Cambodia by maintaining control strategies for humans such as biyearly UT or yearly TT with high coverage.
We appreciate the helpful comments of Profs. H. Matsuda, Y. Chigusa, and M. Kirinoki of Dokkyo Medical University. We are indebted to Dr. T. Matsumoto of the National Institute for Rural Engineering for providing Mekong River water level data.
    Fig. 1
    Monthly average rainfall levels (bars) for 5 years during 1997-2001 in Phnom Penh (World Weather Information Service) and monthly average water levels of the Mekong River (line) for 14 years during 1989-2002 in Kratie province, Cambodia (Mekong River Commission) [14].
    kjp-47-1-g001.jpg
    Fig. 2
    Population dynamics of Neotricula aperta on the basis of the Post-Spate Survival hypothesis. (A) The life cycle of N. aperta, (B) The monthly variation of the total snail population [14].
    kjp-47-1-g002.jpg
    Fig. 3
    The basic scheme of the transmission model for S. japonicum showing the transfers among epidemiological classes [4].
    kjp-47-1-g003.jpg
    Fig. 4
    Variations in the infection of S. japonicum in Bohol (Sto. Thomas) for the human-control case with selective mass treatment at 1-year interval with a coverage rate of 50% (solid line), the snail-control case with the use of molluscicides at half-year intervals under the assumption that its effective rate would be 50% (dotted line), and both the human and snail-control case (dashed line), respectively. (A) Variations in prevalence (%) in the human population, (B) Variations in infected snail densities per 1 a (100 m2) [4].
    kjp-47-1-g004.jpg
    Fig. 5
    Variations in the prevalence in humans with 2 control measures. 1: Yearly universal treatment (UT) with a 70% coverage rate for the initial 3 years (solid line), 2: After 3 years of annual UT targeted mass treatment (TT) with a 85% coverage rate (dashed line) [14].
    kjp-47-1-g005.jpg

    Download Citation

    Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

    Format:

    Include:

    Modeling the Dynamics and Control of Transmission of Schistosoma japonicum and S. mekongi in Southeast Asia
    Korean J Parasitol. 2009;47(1):1-5.   Published online March 12, 2009
    DOI: https://doi.org/10.3347/kjp.2009.47.1.1
    Download Citation

    Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.
    Format:
    Include:
    Modeling the Dynamics and Control of Transmission of Schistosoma japonicum and S. mekongi in Southeast Asia
    Korean J Parasitol. 2009;47(1):1-5.   Published online March 12, 2009
    DOI: https://doi.org/10.3347/kjp.2009.47.1.1
    Close

    Figure

    • 0
    • 1
    • 2
    • 3
    • 4
    Modeling the Dynamics and Control of Transmission of Schistosoma japonicum and S. mekongi in Southeast Asia
    Image Image Image Image Image
    Fig. 1 Monthly average rainfall levels (bars) for 5 years during 1997-2001 in Phnom Penh (World Weather Information Service) and monthly average water levels of the Mekong River (line) for 14 years during 1989-2002 in Kratie province, Cambodia (Mekong River Commission) [14].
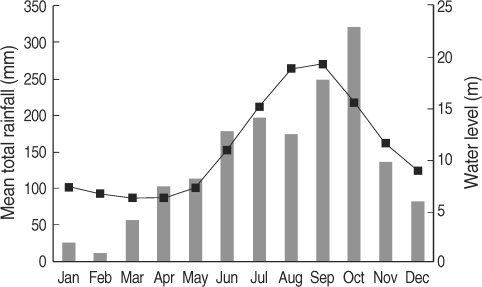
    Fig. 2 Population dynamics of Neotricula aperta on the basis of the Post-Spate Survival hypothesis. (A) The life cycle of N. aperta, (B) The monthly variation of the total snail population [14].
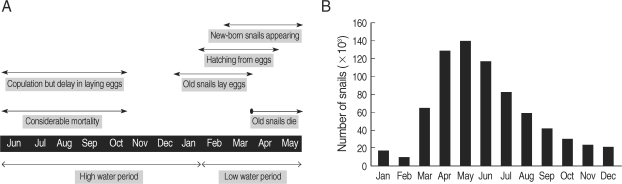
    Fig. 3 The basic scheme of the transmission model for S. japonicum showing the transfers among epidemiological classes [4].
    Fig. 4 Variations in the infection of S. japonicum in Bohol (Sto. Thomas) for the human-control case with selective mass treatment at 1-year interval with a coverage rate of 50% (solid line), the snail-control case with the use of molluscicides at half-year intervals under the assumption that its effective rate would be 50% (dotted line), and both the human and snail-control case (dashed line), respectively. (A) Variations in prevalence (%) in the human population, (B) Variations in infected snail densities per 1 a (100 m2) [4].
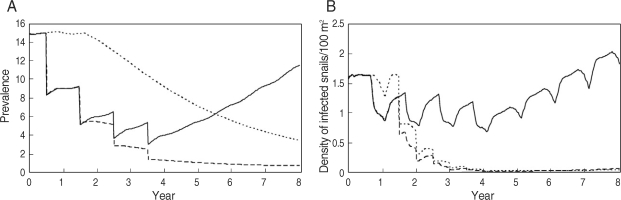
    Fig. 5 Variations in the prevalence in humans with 2 control measures. 1: Yearly universal treatment (UT) with a 70% coverage rate for the initial 3 years (solid line), 2: After 3 years of annual UT targeted mass treatment (TT) with a 85% coverage rate (dashed line) [14].

    Fig. 1

    Fig. 2

    Fig. 3

    Fig. 4

    Fig. 5

    Modeling the Dynamics and Control of Transmission of Schistosoma japonicum and S. mekongi in Southeast Asia
    PHD : Parasites, Hosts and Diseases

    ABOUT

    BROWSE ARTICLES

    EDITORIAL POLICIES

    FOR CONTRIBUTORS

    © The Korean Society for Parasitology and Tropical Medicine.